Dynamic response can be studied by examining a simple system — that of a single-degree-of-freedom oscillator, as shown in Figure 4-16.
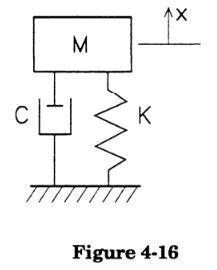
The single-degree-of-freedom oscillator consists of a mass M attached to ground by a spring
with a stiffness K and a dashpot with a damping value of C. The spring pulls on the mass
with a force proportional to its extension or contraction (or the displacement of the mass);
the dashpot provides a frictional force proportional to the velocity of the mass. Any
unbalanced force accelerates the mass. The behavior of a single degree-of-freedom oscillator can then be described by the dynamic equation of motion:

This equation cannot be explicitly solved, unless the damping term, C, is zero and the
imposed load is harmonic (i.e., of the form F(t) = asinb(t+c)). Therefore, the damping value is often dropped (since it is usually small) in order to simplify the equation. The equation
can be simplified further by taking the simplest external harmonic load — a load of zero. If
there is no external load, and damping is approximately zero, the equation describes the free vibration of an undamped single-degree-of-freedom oscillator:

The system characteristics of a single degree-of-freedom oscillator can be completely
described by its natural frequency and its damping value. System response can be
determined once the Dynamic Load Factor (as a function of the natural frequency and
damping value) for the applied load is known.
Read More:
Located in Calgary Alberta, We offer our Piping Engineering Services, Skid Design Services, Pipeline Engineering Services and Structural Engineering Services across Canada. To get our Piping Stress Analysis Services, please contact our Engineering company.
Our professional piping stress engineers have a bachelor's and Masters degree in mechanical / structural engineering and province license (P.Eng.) in Alberta, Saskatchewan, British Columbia and Ontario. We review, validate, certify and stamp piping and structural packages. Also check Industries We Serve.
